Bloom Filter

当我们写爬虫应用的时候，有一件事情是值得我们仔细考虑的，在抓取网上数据的时候，我们的爬虫会沿着当前爬取的网页中的链接继续进行深度优先搜索或者广度优先搜索，但是很显然，这些链接形成的拓扑图肯定不是一个有向无环图，所以肯定会重复抓取某些网页，这肯定不是我们所想要的，为了避免重复抓取导致的返工，我们不加思索的增加了一个 map 来存储当前已经被抓取过的url，这在要求抓取的url数量较少的时候或许是一个不错的解决方案，但是一旦我们要抓取亿级别的url数量时（在现在这种自媒体爆发的时代还是很正常的一件事情），假设我们要抓取的url平均大小是20字节，那么不考虑其他开销，1亿个url需要消耗的内存就是20GB，这显然
是不现实的。我们需要一种更加优化的解决方案。

上述的问题可以抽象为，给定一个元素E，问它是否存在于给定的集合S中，上述使用 map 的存储导致空间开销过大的主要原因就是我们需要存储原来的url，那有没有一种方法不存储每条消息而可以知晓它是否存在于特定的集合中呢，答案就是 Bloom Filter。

Bloom Filter 是一个空间和时间都非常高效的数据结构，它解决的问题也非常简单，就是用于查询特定元素是否存在于某个集合当中，但是这种高效是引入错误率的基础上的高效，下面我们引入 BloomFilter 的两个特性。

• False Positive

Bloom Filter 可能会出现 False Positive 的概率，就是指查询特定元素E是否存在于集合E中，真实情况是E不存在，但是 Bloom Filter 却出现了误判，当 Bloom Filter 存储的元素越多，出现误判的概率也就会越大（一般来说会把误判率控制在可以接受的范围内），这是由 Bloom Filter 本身的特性造成的。

• False Negative

False Negative 指的是元素E本来存在于集合S中，但是 Bloom Filter却出现误判，认为元素E并不存在于集合S中，这种情况是绝对不会出现的，这也是由Bloom Filter 本身的特性决定的。

Bloom Filter实现的思路非常简单，它主要由两个元素组成。

1. 一张位图，决定了 BloomFilter 在空间上是高效的。
2. 多个哈希函数，决定了 BloomFilter 是查询时间上是高效的，理论上的时间复杂度是 O(1)。

下面这张图就大概描述了 Bloom Filter 实现的大致思路，我们来简单过一遍。

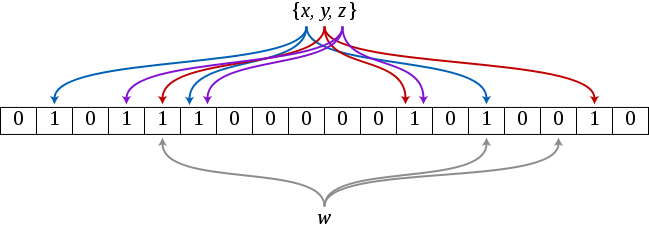
假设当前由集合 S: {x, y, z} ，我们需要查询元素w是否存在于集合S中，第一步应该是位图的构建，位图开始是是一张全部为0的数组，当第一个元素x进入时，程序会通过 Bloom Filter 的所有哈希函数计算出哈希函数对应的哈希值，并将哈希值对应位图的相应位置都设置为1，y和z同理，也就是说此时位图的某些地方已经被设置为1了，但是其余地方都是0。此时我们需要查询元素w是否存在于集合S中，先利用 Bloom Filter 的所有哈希函数计算出相应的哈希值，并利用哈希值查询对应的位图中元素是否都为1，如果都为1，那么则说明元素w可能存在于该集合中，但是只要有一个位置为0，就可以直接判定该元素不存在于该集合中。

下面是 Bloom Filter 的简单实现，bitmap 就是位图，k 是哈希函数的个数，n 是当前存储的元素的个数，当然这里存储的意思并不是把整个元素存储下来，而是在位图中进行标记的意思，m 是整个 Bloom Filter 或者说位图的大小。

type BloomFilter struct {
    bitmap []bool
    k      int
    n      int
    m      int
    hashfn hash.Hash64
}

func NewBloomFilter(numHashFuncs, bfSize int) *BloomFilter {
    bf := new(BloomFilter)
    bf.bitmap = make([]bool, bfSize)
    bf.k, bf.m = numHashFuncs, bfSize
    bf.n = 0
    bf.hashfn = fnv.New64()
}

getHash 就是利用 Bloom Filter 中事先定义的哈希函数计算对应的多个哈希值，这里可以挑选抗碰撞性较好的哈希函数来提高我们程序的鲁棒性。

func (bf *BloomFilter) getHash(b []byte) (uint32, uint32) {
    bf.hashfn.Reset()
    bf.hashfn.Write(b)
    hash64 := bf.hashfn.Sum64()
    h1 := uint32(hash64 & ((1 << 32) - 1))
    h2 := uint32(hash64 >> 32)
    return h1, h2
}

Add 将元素 e 加入 Bloom Filter 中。

func (bf *BloomFilter) Add(e []byte) {
    h1, h2 := bf.getHash(e)
    for i := 0; i < bf.k; i++ {
        ind := (h1 + uint32(i)*h2) % uint32(bf.m)
        bf.bitmap[ind] = true
    }
    bf.n++
}

Check 检查特定元素 e 是否存在于 Bloom Filter 中。

func (bf *BloomFilter) Check(e []byte) bool {
    h1, h2 := bf.getHash(e)
    result := true
    for i := 0; i < bf.k; i++ {
        ind := (h1 + uint32(i)*h2) % uint32(bf.m)
        result = result & bf.bitmap[ind]
    }
    return result
}

函数 FalsePositiveRate() 可以计算 Bloom Filter 出现 False Positive 的概率，这个公式有严格的数学证明，有兴趣的同学可以参考一下它的证明过程，我们现在只需要掌握一点就可以了，就是它存储的元素个数（n）越多，它出现 False Positive 的概率也就越大。但只要调整合适的m 和 k 的值，就可以把错误率控制在可以接受的范围内。

func (bf *BloomFilter) FalsePositiveRate() float64 {
    return math.Pow((1 - math.Exp(-float64(bf.k*bf.n) / float64(bf.m))), float64(bf.k))
}